
Zadanie Podział naszyjnika (pod)
Pomóż nam usprawnić bazę zadań!
Liczba osob: 78
Liczba osob na 100 punktow: 26
Sredni wynik: 52.7564
Podział naszyjnika
Limit pamięci: 128 MB
Mamy naszyjnik złożony z  koralików, z których każdy jest jednego z
koralików, z których każdy jest jednego z 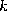 rodzajów.
Koraliki numerujemy liczbami całkowitymi od
rodzajów.
Koraliki numerujemy liczbami całkowitymi od 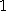 do
do  . Koralik o numerze
. Koralik o numerze 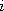 sąsiaduje w naszyjniku z koralikami o numerach
sąsiaduje w naszyjniku z koralikami o numerach
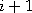 oraz
oraz 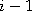 (o ile koraliki o takich numerach istnieją), a ponadto koraliki o numerach
(o ile koraliki o takich numerach istnieją), a ponadto koraliki o numerach 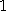 oraz
oraz  również sąsiadują ze sobą.
Chcemy podzielić naszyjnik dwoma cięciami na dwie niepuste części
tak, aby każdy rodzaj koralika występował dokładnie w jednej z części
(tzn. jeśli jedna z części zawiera koralik rodzaju
również sąsiadują ze sobą.
Chcemy podzielić naszyjnik dwoma cięciami na dwie niepuste części
tak, aby każdy rodzaj koralika występował dokładnie w jednej z części
(tzn. jeśli jedna z części zawiera koralik rodzaju  , to druga część nie może zawierać żadnego koralika rodzaju
, to druga część nie może zawierać żadnego koralika rodzaju 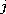 ).
Na ile sposobów możemy to zrobić oraz jaka jest minimalna
różnica długości otrzymanych części?
).
Na ile sposobów możemy to zrobić oraz jaka jest minimalna
różnica długości otrzymanych części?
Wejście
Pierwszy wiersz standardowego wejścia zawiera dwie liczby całkowite  i
i 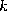 (
(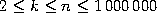 )
oddzielone pojedynczym odstępem, oznaczające długość naszyjnika i liczbę rodzajów koralików. Rodzaje koralików
numerujemy liczbami od 1 do
)
oddzielone pojedynczym odstępem, oznaczające długość naszyjnika i liczbę rodzajów koralików. Rodzaje koralików
numerujemy liczbami od 1 do 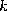 .
Drugi wiersz wejścia zawiera ciąg
.
Drugi wiersz wejścia zawiera ciąg  liczb całkowitych
liczb całkowitych 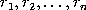 (
( )
pooddzielanych pojedynczymi odstępami; liczba
)
pooddzielanych pojedynczymi odstępami; liczba 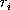 oznacza rodzaj koralika o numerze
oznacza rodzaj koralika o numerze 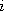 .
Możesz założyć, że każdy rodzaj koralika wystąpi w naszyjniku co najmniej raz.
.
Możesz założyć, że każdy rodzaj koralika wystąpi w naszyjniku co najmniej raz.
W testach wartych łącznie 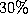 punktów zachodzi dodatkowy warunek
punktów zachodzi dodatkowy warunek 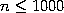 .
.
Wyjście
Pierwszy i jedyny wiersz standardowego wyjścia powinien zawierać dwie liczby całkowite oddzielone pojedynczym odstępem. Pierwsza z nich ma oznaczać liczbę sposobów, na jakie można podzielić naszyjnik (możesz założyć, że dla danych wejściowych co najmniej jeden podział jest możliwy). Druga liczba ma oznaczać minimalną różnicę długości otrzymanych części.
Przykład
Dla danych wejściowych:
9 5 2 5 3 2 2 4 1 1 3
poprawną odpowiedzią jest:
4 3
Wyjaśnienie do przykładu:
Są cztery możliwe podziały; krótsza część może zawierać koraliki 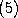 ,
, 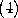 ,
, 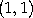 lub
lub  .
W ostatnim przypadku uzyskujemy optymalną różnicę długości
.
W ostatnim przypadku uzyskujemy optymalną różnicę długości 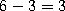 .
.
Testy "ocen":
- 1ocen:
krótki naszyjnik z dwoma możliwymi podziałami (
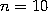 );
);
- 2ocen:
naszyjnik długości
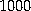 , wszystkie koraliki mają różne kolory, wszystkie podziały są poprawne;
, wszystkie koraliki mają różne kolory, wszystkie podziały są poprawne;
- 3ocen:
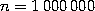 ,
, 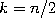 , naszyjnik postaci
, naszyjnik postaci 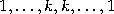 .
.
Autor zadania: Jacek Tomasiewicz.
<Wyślij rozwiązanie> [0/100]Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English